Introduction
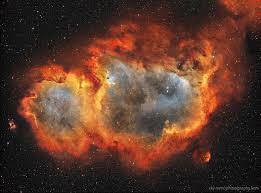
Soul Nebula, also known as Westerhout 5, Sharpless 2-199, Sh2-199, LBN 667 and IC 1848, is an Emission Nebula located in The Cassiopeia Constellation. Soul Nebula is located 7500 Light Years from Earth. Soul Nebula contains gigantic cavities that were carved out by radiation and winds from the region's most largest stars. Soul Nebula has a neighbor Nebula known as Heart Nebula and so together they are known as Heart and Soul or Heart and Soul Nebulae.

Introduction
Pistol Nebula is an emission nebula located in the Sagittarius Constellation. Pistole Nebula is located 25,000 Light Years from Earth. Pistol Nebula has a mass of 9.3 Solar Masses. Inside The Pistol Nebula is the extremely luminous star, Pistol Star, which is 1.6 Million fold the brightest of The Sun. Pistol Nebula is a Quintuplet Cluster located almost in the center of The Milky Way Galaxy. 

Introduction
Coalsack Nebula, also known as Coalsack, Southern Coalsack, il Canopo fosco, The Dark Canopus, Macula Magellani, Magellanic Spot, Yutu, Caldwell 99, C99 and Black Magellanic Cloud, is a Dark Nebula/Absorption Nebula located in The Crux Constellation. Coalsack Nebula is located 590 Light Years from Earth. A Dark Nebula or Absorption Nebula is an interstellar cloud that is extremely dense, to the point that it obscures the light from objects behind it, such as background stars and emission or reflection nebulae. Coalsack Nebula has a radius pf 30 to 35 Light Years. The Coalsack Nebula was discovered in 1499 AD by Spanish Explorer Vicente Yáñez Pinzón. Italian Explorer Amerigo Vespucci, who The Americas are named after, name it il Canopo fosco or The Dark Canopus. Coalsack Nebula can be seen in space with the naked eye, where it will be seen as a dark splat hindering the light of stars in The Milky Way. In Ancient Inca, Incan Astronomers knew this Nebula as Yutu, or Tinamou, a partridge -like southern bird. 

Introduction
Cotton Candy Nebula, also known as IRAS 17150-3224, is a Protoplanetary Nebula, a Post Asymptotic Giant Branch Star and a Reflection Nebula. An Asymptotic Giant Branch is a region of the Hertzsprung–Russell diagram populated by evolved cool luminous stars. Cotton Candy Nebula is located in The Ara Constellation. Cotton Candy Nebula is in the process of becoming a planetary nebula, but of now, it is but a gaseous nebula with Post ASG Stars.

Introduction
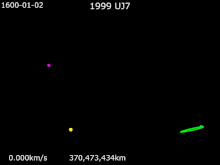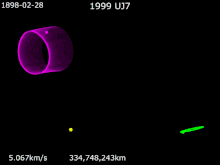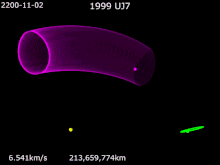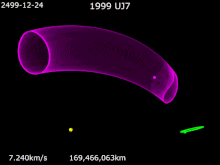
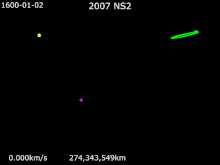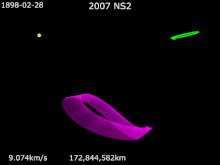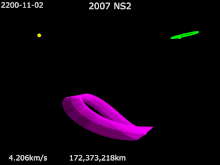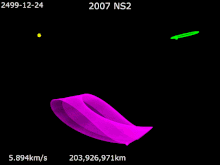
Mars Trojans basically are a Team of Trojan Objects that share an orbit with Mars around The Sun. The Mars Trojans can be seen 60 degrees on front of and behind Mars's two Lagrangian Points. As explain in Jupiter Trojans, Trojans, Trojan Asteroids or Trojans, are a Giant Team of Asteroids that share the same orbit around The Sun and the relative planet's orbit. The Origins of The Mars Trojans are cloudy but speculation leads to them coming from Primordial Astronomical Objects that were leftover in the formation of Mars. Another Theory on The Origin of The Mars Trojans are Asteroids falling into orbits within The Lagrangian Points eons ago. 
Groups of Mars Trojans
The Leading Group known as L4 has: (121514) 1999 UJ7 †. The Trailing Group known as L5 has: 5261 Eureka †, (101429) 1998 VF31 †, (311999) 2007 NS2 †, (385250) 2001 DH47, 2011 SC191 and 2011 UN63. One Candidate for being a Mars Trojans is 2011 SL25.

Introduction
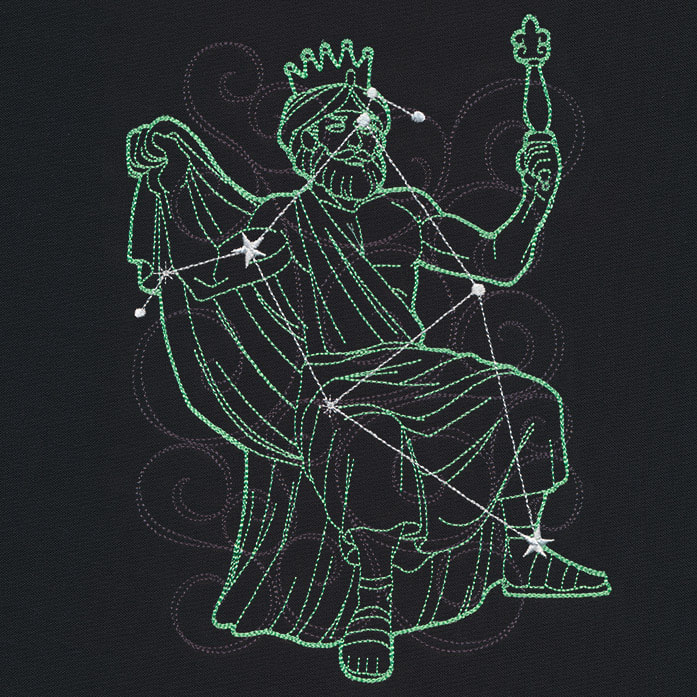
The King, also known as King, Cepheus and King Cepheus, is a Constellation in Space that borders Draco, Cassiopeia, Ursa Major, Lacerta, Cygnus and Camelopardalis. The King has 7 Main Stars and 1 of its Stars has planets. The brightest star in King is Alderamin (Alpha Cephei).
Information about The King
The Stars within The King are: Alpha Cephei, Mu Cephei, Beta Cephei, VV Cep, Kruger 60, Xi Cep, V381 Cep, Eta Cephei, Zeta Cephei, 2 Ursae Minoris, Iota Cephei, V354 Cep, RW Cep, Epsilon Cephei, Nu Cephei, V419 Cephei, WR 156, Gliese 809, WISEPA J031325.96+780744.2, HD 221525, Rho2 Cep, Theta Cephei, Omicron Cephei, HD 217382, HD 216446, Pi Cephei, HR 9038, Kappa Cephei, PV Cep, HR 7955, 9 Cep, 11 Cep, HD 12467, HR 8442, 13 Cep, 19 Cep, WX Cep, S Cep, HD 4853, IV Cep, HD 202214, HD 18778, HD 19978, 16 Cep, VW Cep, W Cep, 24 Cep, Lambda Cephei, 7 Cep, U Cep and X Cep. The Galaxies with The King are: NGC 6946, Palomar 1, 3C 61.1, NGC 2300, NGC 2276, IC 455 and IC 1502.
More Information about The King
The King was First Introduced in The 100s AD by The Roman World Astronomer Ptolemy. The King is Based off The Classical World King of Aethiopia, King Cepheus who is The Father of Andromeda and The Husband of Queen Cassiopeia.  

Introduction
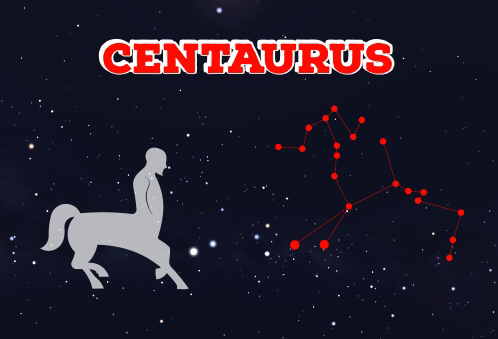
Centaurus, also known as Centaur, The Centaur or The Bison Man, is a constellation in space that borders Antlia, Carina, Crux, Musca, Vela, Circinus, Hydra, Libra and Lupus. Centaurus has 11 Main Stars and 15 of its stars has planets. The brightest star in Centaurus is Alpha Centauri. 
Information about Centaurus
Stars within Centaurus are: Alpha Centauri, Alpha Centauri A, Alpha Centauri B, Beta Centauri, Proxima Centauri, Theta Centauri, Gamma Centauri, Epsilon Centauri, Iota Centauri, SN 1986G, BPM 37093, HR 5171,  Rho Centauri, Sigma Centauri, Pi Centauri, Mu Centauri, Delta Centauri, HD 102117, HD 117618, Przybylski's Star, PDS 70, GJ 3737, V1400 Centauri, Nu Centauri, V810 Cen, HD 105382, HD 129116, HD 125823, V744 Cen, HD 113538, V803 Cen, V842 Cen, V752 Cen, J Cen, Eya Centauri, H Cen, HD 101930, HD 117207, HD 114729, HD 121504, HD 1143866, HD 103197, Lambda Centauri, Tau Centauri, Psi Centauri, R Cen, Chi Centauri, 1 Cen, Kappa Centauri,HD 102365, 4 Cen, A Centauri and Zeta Centauri. Galaxies within Centaurus are: Centaurus A, Messier 83, NGC 4945, NGC 5253, NGC 5408, NGC 5102, NGC 5237, NGC 4696, NGC 5264, HIDEEP J1336-3321, NGC 4650A, NGC 4709, ESO 325-G004, ESO 269-57, NGC 4622, ESO 444-46, IRAS 13224-3809, NGC 4603 and NGC 5291. 
More Information about Centaurus
Centaurus as a constellation was Officially Introduced in The 100s AD by Roman World Astronomer Ptolemy but its recognition as a constellation dates back to The Classical World in 4th Century BC and the 3rd Century BC. Centaurus is based off The Centaur, a creature from The Classical World that is Half Man on top and Half Steed on the bottom. In Ancient Babylonia, this same constellation was seen as The Bison Man. 

Introduction
Green Bean Galaxy, also known as J0113+0106 and J1155-0147, are two galaxies that are a rare quasar ionization echos. Ionization Echos or Light Echo are physical phenomenon that are caused by a light reflection off a distant surface from some sort of source that is delayed relative to the distance of said object. GBGs or Green Bean Galaxies are extremely rare, so rare, that in fact, on-average, only one is seen every 1.3 Billion Light Years across in a cube. They are known as Green Bean Galaxies because of their observable green color. Green Bean Galaxies was discovered by German Astronomer Mischa Schirmer. 

Introduction
Carina, also known as The Keel, The Hull, The Hull of a ship and The Keel of Ship, is a constellation in space that borders Centaurus, Volans, Vela, Puppis, Pictor, Musca and Chamaeleon. Carina has 9 Main Stars and 11 of its stars has planets. The brightest star in Carina is Canopus (Alpha Carinae). 
Information about Carina
Stars within Carina are: Alpha Carinae (Canopus), Beta Carinae, Epsilon Carinae, Iota Carinae, V382 Car, HD 84810, V337 Car, HR 4102, PP Car, Omega Carinae, OGLE2-TR-L9, Chi Carinae, V344 Car, HD 93205, LHS 288, V399 Car, OGLE-TR-182, OGLE-TR-211, Sher 25, WR 25, OGLE-TR-123, V528 Car, WR 22, V372 Car, NG 3603-A1, HR 3126, HR 4138, V345 Car, DENIS J081730.0-615520, QZ Car, CPD−57°2874, WR 31a, Innes' Star, WR 21a, WR 30a, WR 42e, V357 Car, WISE J080822.18-644357.3, R Car, V376 Car, HD 88366, HD 90953, V533 Car, HD 69863, HD 97950, HD 83183, HD 63765, V343 Car, HD 66194, N Car and Upsilon Carinae B. 
More information about Carina
Carina was a member of a larger constellation in times gone by. Carina was once a piece of ship, but not just any ship, it was a piece of the great ship known as Argo Navis which was the ship rode by Jason and The Argonauts. Carina would not be its own constellation until 1763, when French Astronomer Abbe' Nicolas-Louis de Lacaille separated it from Argo Navis into its own constellation. 

Introduction
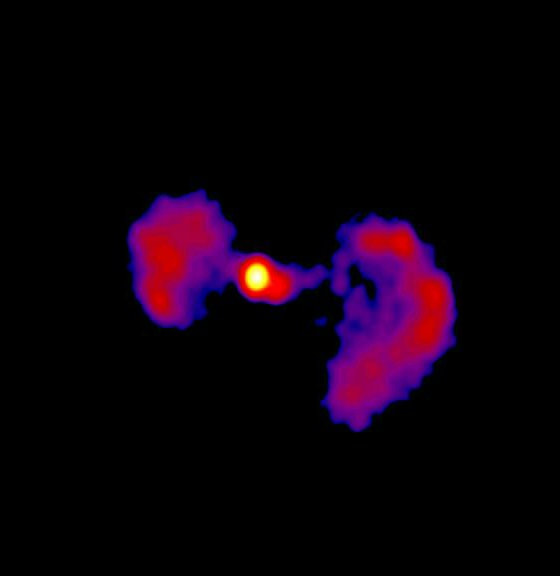
Star Wars Galaxy, also known as Star Wars and TXS 0128+554, is a Emission Galaxy located in the Cassiopeia Constellation. Star Wars Galaxy is located 500 Million Light Years from Earth. Star Wars Galaxy was discovered in 2015 by NASA and in 2020 was noted as looking like Darth Vader's Tie Fighter in Star Wars, prompting The World Aloha to officially name TXS 0128+554, Star Wars Galaxy of August 28th, 2020 a little after 8 Am CST. Star Wars Galaxy is held together by a Supermassive Black Hole. Star Wars Galaxy was discovered using NASA's Fermi Gamma-ray Space Telescope where TXS 0128+554 was discovered due it being a faint source of gamma ray energy. Later on, NASA zoomed in on TXS 0128+554 One Million fold and that's where it looks like a Star Wars Tie Fighter. So now The World Aloha Officially names TXS 0128+554, Star Wars Galaxy!

Introduction
Camelopardalis, also known as Giraffe, The Giraffe, Camelopardali Hevelii and Camelopard, is a constellation in space that borders Draco, Ursa Major, Ursa Minor, Lynx, Auriga, Perseus, Cepheus and Cassiopeia. Camelopardalis has 2 to 8 Main Stars and 4 of its stars has planets. The brightest star in Camelopardalis is Beta Camelopardalis. 
Information about Camelopardalis
Stars within Camelopardalis are: Alpha Camelopardalis, Beta Camelopardalis, Gamma Camelopardalis, Struve 1694, 11 Cam, 7 Cam, 12 Cam, 3 Cam, 43 Cam, CS Cam, HD 33564, 1 Cam, 23 Cam, VZ Cam, 42 Cam, 14 Cam, HD 104985, 2 Cam, PSR B0320+54, 5 Cam, 16 Cam, Gliese 445, 18 Cam, 53 Cam, XO-3, 2MASS 0532+8246, 4 Cam, HD 32518, NGC 2363-V1, 17 Cam, 19 Cam, 36 Cam, 15 Cam, 47 Cam, 51 Cam, 49 Cam, 37 Cam, 29 Cam, 24 Cam, 31 Cam, 8 Cam, 40 Cam, 30 Cam, 26 Cam, Z Cam, BK Cam, BE Cam, U Cam, HD 42818, HD 49878 and HD 21389. Galaxies within Camelopardalis are: IC 342, NGC 2403, NGC 1569, NGC 2655, NGC 1573, NGC 2366, MS 0735.6+7421, MACS J0647.7+7015, NGC 2146, NGC 2363 and NGC 2523. 
More Information about Camelopardalis
Camelopardalis was introduced in 1612 by Dutch-Flemish Astronomer Petrus Plancius.

Introduction
Caelum, also known as Chisel, the engravers' chisel and Caelum Sculptorium, is a constellation in the night sky that borders Dorado, Columba, Lepus, Eridanus, Horologium and Pictor. Caelum has 4 Main Stars and 1 of its stars has planets. The brightest star in Caelum is Alpha Caeli. 
Information about Caelum
Stars within Caelum are: Alpha Caeli, Beta Caeli, X Cae, Gamma1 Cae, Delta Caeli, Zeta Caeli, Nu Caeli, RR Caeli, Lambda Caeli, RV Cae, HD 30876, R Cae, Z Cae, S Cae, V Cae, Y Cae, W Cae and T Cae. Galaxies inside of Caelum are: NG 1679, IC 2106 and NGC 1571. 
More Information about Caelum
Caelum was introduced in The 1750's AD by French Astronomer Nicolas-Louis de Lacaille who originally received the name Caelum Sculptorium or The Engravers' Chisel. It would later be changed to its current name, Caelum, by English Astronomer Francis Baily. 

The Worlds of The World as vast and diverse. Whether a World as in a planet, a world as in a tradition, a world as in a collection of things; whether The Material or Ideological and Immaterial, the variation of worlds seems to be unquantifiable. Each World has its own unique set of quirks that sets it apart and bring it together with other worlds. Is it even possible to know all worlds? Nay, for it takes a lifetime to even know one world completely. One World alone is so unique and pack with information or physical detail, that one can never know everything about a World. Even one is a Master of knowledge to a particular world, The Master is not Omniscient about the world he has Mastery of. So how can one man be Omniscience? For knowing all worlds would mean one must know all details of the past, present and full future of every single world and worlds within those worlds and in betweens all at once. This tasks seems to be impossible from a logical standpoint and the capacity of man's brain at the present is too limited to be omniscience. A man's brain would need to be unlimited in capacity it seems for him to know all things ever, are and ever will be. And yet the diverging structure of world into new and separating worlds would seem to make even the unlimited brain limited in respects to knowing all things. Nonetheless, man thrives to gain knowledge and wisdom despite knowing that he cannot know all. And perhaps this is a good thing, for what other purpose can one's brain function, besides retention, if one's brain is omniscience, if one knows everything about The World.

Introduction
Bootes, also known as Boötes, Herdsman, Plowman and Ox-Driver, is a constellation in the night sky that borders Draco, Virgo, Hercules, Ursa Major, Corona Borealis, Canes Venatici, Coma Berenices and Serpens Caput. Bootes has 7 to 15 Main Stars and 10 of its Stars has planets. The brightest Star in Bootes is Arcturus (Alpha Boötis).
Information about Bootes
Stars within Bootes are: Alpha Boötis (Arcturus), Eta Boötis, Gamma Boötis, Beta Boötis, Tau Boötis, 38 Boo, Theta Boötis, Iota Boötis, Delta Boötis, Kappa Boötis, 44 Boo, Psi Boötis, Sigma Boötis, 22 Boo, Lambda Boo, 1 Boo, 45 Boo, 47 Boo, 24 Boo, 10 Boo, Omega Boötis, Pi Boötis, 34 Boo, 6 Boo, 20 Boo, 46 Boo, 12 Boo, Xi Boötis, HD 131496, GJ 526, HD 128311, WASP-14, 101 Virginis, HAT-P-4, 31 Boo, TVLM 513-46546, SDSS J1416+1348, Zeta Boötis, Rho Boötis, 2MASS 1503+2525, HD 136418, HD 132406, 9 Boo, 39 Boo, Upsilon Boötis, HD 125351, 7 Boo, 40 Boo, 3 Boo and 18 Boo. Galaxies within Bootes are: Bootes I, 3C 295, MCG+01-02-015, IC 883, Bootes II, Bootes III, Canes Venatici II, Messier 94, Canes Venatici I, DDO 190, Pisces I, MS 1512-cB58, Virgo I, NGC 5466, Phoenix II, UGCA 86, Andromeda XIII, UGC 9128, Andromeda XXIV, Andromeda XVI, Andromeda XVII, Andromeda XXVI, Andromeda XXVIII, Andromeda XV, Andromeda XXV, Andromeda XXIII, Andromeda XXIX, Andromeda XIV and Andromeda XX. 

Introduction
Auriga, also known as The Charioteer, is a constellation in the night sky that borders Gemini, Lynx, Perseus, Taurus and Camelopardalis. Auriga has 5 to 8 Main Stars and 7 of its stars has planets. The brightest star in Auriga is Capella (Alpha Aurigae). 
Information about Auriga
Stars within Auriga are: Alpha Aurigae (Capella), Epsilon Aurigae, Eta Aurigae, Zeta Aurigae, Iota Aurigae, Theta Aurigae, Delta Aurigae, Æ Aurigae, Nu Aurigae, Lambda Aurigae, Omega Aurigae, HD 49674, HAT-P-9, Chi Aurigae, Kappa Aurigae, Pi Aurigae, Mu Aurigae, 2 Aur, Gliese 268, HD 45350, 9 Aur, RT Aur, Xi Aur, HD 40979, Tau Aurigae, V538 Aurigae, GD 66, V433 Aur, V352 Aur, Upsilon Aurigae, 26 Aur, HD 43691, WASP-12, V394 Aur, 63 Aur, V420 Aur, KELT-2A, 16 Aur, UGPS J0521+3640, UU Aur, HD 30453, Omicron Aurigae, 14 Aur, Sigma Aurigae, R Aur, Phi Aurigae, Psi2 Aur, AB Aurigae and 36 Aur. Galaxies within Auriga are: NGC 1857, NGC 2208 and Palomar 2. 

Introduction
Ara, also known as The Altar, is a constellation in the night sky that borders Pavo, Apus, Corona Australis, Norma, Scorpius, Telescopium and Triangulum Australe. Ara has 8 Main Stars and 7 of its star has planets. The brightest star in Ara is Beta Arae. 
Information about Ara
Stars within Ara are: Alpha Arae, Beta Arae, Gamma Arae, Zeta Arae, Mu Arae, Delta Arae, Westerlund 1-26, Eta Area, Gliese 674, HD 156411, HD 154857, Gliese 676, HD 154672, HD 152079, Epsilon1 Ara, Theta Arae, HD 158220, GX 339-4, V539 Arae, XTE J1650-500, CXOU J164710.2−455216, HD 149989, HD 153261, HR 6384, HD 160342, 2MASS J18082002−5104378, Westerlund 1-20, SGR 1627-41, Westerlund 1-237, Westerlund 1-75, CD-59 6479, Sigma Arae, Lambda Arae, Iota Arae Pi Arae, Kappa Arae, HD 150136, R Ara, HD 157661, HD 153053, HD 158476, HD 165493, HD 156768, HD 150576, HD 151967, HD 152082, HD 156091, HD 153221, HD 153791 and HD 157819. Galaxie inside of Ara are: NGC 6362, NGC 6215, NGC 6221, NGC 6300 and NGC 6379. 
​More Information about Ara
Ara was introduced in The 100's AD by Roman World Astronomer Ptolemy. It later became an Official Constellation by The International Astronomical Union in Today's World. 

Introduction
Aquarius, also known as The Water Bearer, is a constellation in space that borders Pisces, Pegasus, Equuleus, Delphinus, Aquila, Capricornus, Piscis Austrinus, Sculptor and Cetus. Aquarius has 10 to 22 Main Stars with 12 of its stars possessing planets. The brightest stars in Aquarius is Sadalsuud (Beta Aquarii).
Information about Aquarius
Stars within Aquarius are: Alpha Aquarii, Beta Aquarii, Gamma Aquarii, Delta Aquarii, Zeta Aquarii, Epsilon Aquarii, Theta Aquarii, 91 Aqr, Lambda Aquarii, Gliese 876, Nu Aquarii, Iota Aquarii, Eta Aquarii, Gliese 849, Pi Aquarii, R Aqr, Kappa Aquarii, HD 215152, WASP-6, 1 Aquarii, 88 Aqr, HD 210277, WASP-47, HD 222582, Mu Aquarii, Sigma Aquarii, Phi Aquarii, Psi2 Aqr, 4 Aqr, Xi Aquarii, Upsilon Aquarii, 3 Aqr, 3 Aqr, K2-138, K2-28, EZ Aqr, 25 Aqr, Sneden's Star, Tau2 Aqr, Fomalhaut C, LS IV- 14 116, WASP-69, WASP-75, 99 Aqr, 94 Aqr, Psi3 Aqr, 47 Aqr, 106 Aqr, 107 Aqr, 

Introduction
Andromeda, also known as The Chained Lady, is a constellation in Space that borders Cassiopeia, Pegasus, Perseus, Pisces, Lacerta and Triangulum. Andromeda has 16 Main Stars and 12 of its stars has planets. The brightest star in Andromeda is Alpheratz (Alpha Andromedae).
Information About Andromeda
Stars inside Andromeda are: Alpha Andromedae, Beta Andromedae, Upsilon Andromedae, Delta Andromedae, Mu Andromedae, 51 Andromedae, Xi Andromedae, Kappa Andromedae, 56 And, 14 And, Ross 248, HD 16175, Zeta Andromedae, WASP-1, Nu Andromedae, Phi Andromedae, 32 And, V455 Andromedae, Psi Andromedae, HD 5608, HD 15082, RX And, 36 And, HAT-P-53, HD 1605, Omicron Andromedae, NGC 206, Groombridge 34, Lambda Andromedae, Epsilon Andromedae, Pi Andromedae, R And, 28 And, Rho Andromedae, HAT-P-6, UY And, Tau Andromedae, 3XMM J004301.4+413017, TW And, BQ And, CI And, IU And, FI And, AA Andromedae, CV And, VY And, DP And, V603 And, HD 556, KO And and HL And. Galaxies inside Andromeda are: Andromeda (Andromeda Galaxy), Andromeda I, Andromeda II, Andromeda III, Andromeda IV, Andromeda V, Andromeda X, Messier 32, Messier 110, NGC 68, NGC 891, NGC 147, NGC 185, Cassiopeia Dwarf, Andromeda XXII, Donatiello I, Pegasus Dwarf Spheroidal Galaxy, NGC 404, 3C 66B, NGC 27, NGC 80, NGC 71, NGC 83, NGC 214, NGC 21, NGC 93, NGC 48, NGC 20, NGC 97, NGC 76, NGC 43, NGC 69, NGC 49, NGV 74, NGC 94, NGC 70, NGC 13, NGC 39, NGC 67, NGC 79, NGC 86, NGC 72, NGC 81, NGC 160, NGC 90, NGC 184, NGC 19, NGC 109, NGC 19, NGC 108, NGC 112, NGC 149 and NGC 169. 
More Information about Andromeda
Andromeda's origins dates back to The Classical World Tradition and the particular stars of Andromeda have been seen as a woman in more Ancient times in Babylonia. In The Classical World Andromeda was also known as Persea, The Wife of Perseus and Cepheis, The Daughter of Cepheus. In The Main Classical World Tradition, Andromeda is the daughter of The Queen of Ethiopia, Cassiopeia. Queen Cassiopeia would boast about Andromeda as her most fair daughter who was even more beauteous than the Sea Nymphs known as The Nereids. This peeved The god of The Sea, Storms and Horses Poseidon who then commanded The Sea Monster Cetus to attack Ethiopia. The Father of Andromeda, Cepheus, went forth to Omniscience Oracle of Ammon for the answer of what he must do to save his Kingdom, Ethiopia. The Oracle of Ammon told Cepheus that he must sacrifice his daughter, Andromeda, in order to save his kingdom. Hearing this, Cepheus hastily went and chained Andromeda next to the sea in order to die at the will of Poseidon. She seemed to be doomed until The Hero Perseus rescued her from her sealed fate. He did this by using Medusa severed head to turn the monster Cetus to stone. In other version Perseus used a diamond sword to slice and kill Cetus. Either way, after this event Perseus and Andromeda went forth and married one another and had 9 offspring. When Andromeda passed away, Athena placed her in the night sky to honor her where she lay to this day. 

Introduction
Sculptor, also known as Apparatus Sculptoris, The Sculptor's Studio or The Sculptor, is a constellation in the night sky that borders Fornax, Phoenix, Cetus, Grus, Aquarius and Piscis Austrinus. Sculptor has 4 Main Stars and 6 of its stars has planets. The brightest star in Sculptor is Alpha Sculptoris. 
Information about Sculptor
Stars inside of Sculptor: Alpha Sculptoris, Beta Sculptoris, Eta Sculptoris, Gliese 1, HD 4208, Delta Sculptoris, HD 9578, WASP-8, R Scu, Zeta Sculptoris, Iota Sculptoris, WD 0137-349, Gamma Sculptoris, HE 2359-2844, Kappa2 Scl, Epsilon Sculptoris, Theta Sculptoris, Kappa1 Scl, Sigma Sculptoris, Mu Sculptoris, Pi Sculptoris, Tau Sculptoris, Xi Sculptoris, Lambda2 Scl, Lambda1 Scl, Magellanic Stream, X Sci, Gliese 58, HD 9770, Y Sci, W Scl, HD 3735, HD 268, V Scl, U Scl, HD 427, Rho Telescopii, Gliese 18, Gliese 46, AV Scl, WASP-45, HD 10002, WZ Scl, HD 224113, VY Scl, GSC 6415-1033, RG 0050-2722, S Scl, Al Scl and T Scl. Galaxies inside of Sculptor are: Sculptor Galaxy (Sculptor Dwarf Irregular Galaxy), NGC 55, NGC 7793, NGC 300, NGC 625 and NGC 247. 

Introduction
Rosette Nebula, also known as Caldwell 49, CTB 21, SH 2-275, is a Multipart Nebula located inside The Monoceros Constellation. Rosette Nebula is located 5200 Light Years from Earth and has a radius of 65 Light Years. The Rosette Nebula is located inside The Milky Way Galaxy. The complex of New General Catalogues that make up Rosette Nebula are NGC 2237, NGC 2238, NGC 2239, NGC 2244 and NGC 2246. Rosette Nebula was discovered in 1784 by British-German Astronomer William Herschel. 

Introduction
The concept of the Blue Avians entered public consciousness in recent years, largely attributed to Corey Goode, a whistleblower who claimed to have had contact with these enigmatic beings. According to Goode, the Blue Avians are higher-dimensional extraterrestrial entities who are part of a broader collective called the Sphere Being Alliance. These beings are said to be focused on assisting humanity in achieving spiritual growth and guiding us towards a more harmonious existence.
Physical Characteristics and Communication
As their name suggests, the Blue Avians are often described as tall, blue-skinned, bird-like beings with large, feathered wings and a strikingly humanoid appearance. Their most distinctive feature is their avian-like head, complete with a beak-like mouth. According to accounts, they primarily communicate telepathically, projecting complex ideas and emotions directly into the recipient's mind.
Teachings and Purpose
The alleged teachings of the Blue Avians emphasize the importance of self-awareness, unity, and spiritual evolution. They purportedly advocate for humanity's transition towards a more enlightened state, marked by a collective commitment to peace, harmony, and coexistence. While the messages seem rooted in positive principles, skepticism arises due to the lack of concrete evidence to support the claims made by Goode and others who have shared similar experiences.
Criticism and Skepticism
Critics argue that the Blue Avians phenomenon lacks credible scientific evidence and is instead a product of a combination of New Age beliefs, ufology, and pseudoscience. The absence of verifiable data, physical evidence, and consensus within the scientific community raises questions about the authenticity of these encounters.
Skeptics suggest that accounts of such encounters could potentially be attributed to psychological factors, including vivid dreams, hallucinations, or even deliberate attempts to deceive for personal gain or attention. Additionally, the proliferation of misinformation and hoaxes in the age of the internet further complicates efforts to separate fact from fiction.
The Cultural Significance of Alien Encounters
While the authenticity of Blue Avian encounters remains in question, the phenomenon reflects a deeper societal yearning for connection, meaning, and the exploration of the unknown. Throughout history, cultures around the world have been captivated by the idea of intelligent extraterrestrial life. Alien encounters, whether real or imagined, serve as a mirror to humanity's aspirations, anxieties, and curiosity about our place in the cosmos.
Conclusion
The notion of encountering extraterrestrial beings, such as the Blue Avians, continues to fuel discussions about the mysteries of the universe and our place within it. While evidence supporting these claims is lacking, the allure of connecting with advanced and benevolent cosmic entities speaks to our inherent desire for enlightenment, unity, and a broader perspective on existence. As technology advances and our understanding of the universe deepens, perhaps one day we will uncover the truth behind these alleged encounters, shedding light on the enduring enigma of the Blue Avians.

Introduction
Seagull Nebula, also known as IC 2177, Sh2-292 and GUM 1, is an Emission Nebula located at the borders of both Monoceros Constellation and Canis Major Constellation. Seagull Nebula is located 3650 Light Years from Earth, Seagull Nebula was discovered by Welsh Astronomer Isaac Roberts. 

Introduction
Holmberg 15A, also known as Abell 85-BCG, is a Supergiant Elliptical Galaxy located inside The Cetus Constellation. Holmberg 15A is The Central Dominant Galaxy in The Abell 85 Galaxy Cluster. Holmberg 15A is located 700 Million Light Years from Earth. Holmberg 15A has a mass of 7 X 10^13 Solar Masses and is 270,000 Light Years. Holmberg 15A contained 5 X 10^12 Stars in its bounds.  Holmberg 15A was discovered in 1937 by Swedish Astronomer Erik Holmberg. Holmberg 15A is believed to have at its center, a Supermassive Black Hole with a mass of 40 Billion Solar Masses. 

Introduction
Galaxy 2535, also known as NGC 2535, UGC 4264, PGC 22957 and Arp 82, is an unbarred spiral galaxy located inside The Cancer Constellation. Galaxy 2535 is characterized by its weak inner ring structure which surrounds its nucleus. This structure emits a green, blue and pink color to the human eye. This structure is likely caused by a companion galaxy NGC 2536.

Introduction
Pegasus, also known as The Winged Horse or The Winged Steed, is a constellation that borders Andromeda, Pisces, Cygnus, Equuleus, Lacerta, Vulpecula, Delphinus and Aquarius. Pegasus has 9 to 17 Main Stars and 12 of its stars has planets. The brightest star in Pegasus is Enif (Epsilon Pegasi).
Information about Pegasus
Stars inside of Pegasus are: Alpha Pegasi (Markab, Marchab), Epsilon Pegasi (Enif), Beta Pegasi (Scheat), Gamma Pegasi (Algenib), 51 Peg, Zeta Pegasi (Homam), Eta Pegasi (Matar), Theta Pegasi (Biham), Mu Pegasi (Sadalbari), Iota Pegasi, Lambda Pegasi, 1 Pegasi, Upsilon Pegasi, Tau Pegasi, Pi2 Peg, Kappa Pegasi, Xi Pegasi, IK Pegasi, HR 8799, 9 Peg, HD 209458, Psi Pegasi, Omicron Pegasi, V391 Pegasi, WASP-10, HAT-P-8, BD+14 4559, WASP-21, Gliese 829, Sigma Pegasi, 55 Peg, WASP-59, 70 Peg, Gliese 880, 32 Peg, AG Peg, 35 Peg, 56 Peg, 2 Peg, Pi1 Peg, 23 Peg, 85 Peg, 78 Peg, Nu Pegasi, Phi Pegasi, Rho Pegasi, Chi Pegasi, HR 8548, LL Peg, HR 8903 and 31 Pegasi. 
More Information about Pegasus
Pegasus was introduced in The 100's AD my Roman World Astronomer Ptolemy. In The Classical World, Pegasus was a Mythical Flying Winged Horse with Magic Powers. Pegasus was born when Medusa's head was chopped off. Pegasus was born from the blood of Medusa. The Father of Pegasus is The Classical World god of Sea, Storms, Earthquakes and Horses, Poseidon. Later on, Pegasus became the trusty steed of Bellerophon, who was the greatest hero and slayer of monsters before the time of Heracles (Hercules).